Solve the Following Systems of Equations `X Y/2 = 4` `X/3 2y = 5` Solve by elimination method,xy/2=4,x/32y=5 Answer Stepbystep explanation The given equations are and which can be rewritten as (1) Ex 34, 1 (Elimination) Solve the following pair of linear equations by the elimination method and the substitution method (i) x y = 5 and 2x – 3y = 4 x y = 5 2x – 3y = 4 Multiplying equation (1) by 2 2(x y) = 2 × 5 2x 2y = 10 Solving

Solved X 7 Y 3 5 X 2 Y 9 6 By Elimination Method Brainly In
X+y/2=4 x/3+2y=5 by elimination method
X+y/2=4 x/3+2y=5 by elimination method- x 2y 5 3x 2 3y 10 solve by elimination method Mathematics TopperLearningcom dzs9yv22 Starting early can help you score better!556MATHFILEFILEMATH Second Method Elimination by addition 3(1 3x 124 = 9 3 3x 2y = 5 3 2 14Y = 14 14 14 J = 1 In egD X Hy = 3 X 4 1 = 3 X = 3 4 556MATHFILEFILEMATH Second Method Elimination by



Solving Simultaneous Equations The Substitution Method And The Addition Method Algebra Reference Electronics Textbook
The elimination method of solving systems of equations is also called the addition method To solve a system of equations by elimination we transform the system such that one variable "cancels out" Example 1 Solve the system of equations by elimination $$ \begin{aligned} 3x y &= 5 \\ x y &= 3 \end{aligned} $$Answer to Solve 2 x 3 y = 14 and 3 x 4 y = 4 by the method of elimination By signing up, you'll get thousands of stepbystep solutions toClick here👆to get an answer to your question ️ Solve by elimination method x y = 5 2x 3y = 4
x = 1 y = 2 Ok So prefer the elimination method, but you can do this with substitution as well First put the equations on top of each other x 2y= 5 2x3y=4 Then find the variable that would be easiest to cancel out I think it's x because you only have to modify one of the equations Let's multiply the first equation by 2 This will allow us to cancel out the two x's in the equations Solve the following system of equations by elimination method 2x 3y = 8;Use the M method to solve the following linear programming problem Minimize C 5x10x15x Subject to 2x3xx (or equal to) 1 x,,x,x>(and equal to) 0 Intermediate Algebra Solve using elimination method
Solve the Given equation in Elimination method and Substitution MethodAre solved by group of students and teacher of Class 10, which is also the largest student community of Class 10Solve the system 3xy=8 and x2y=5 by the elimination method 3xy=8 x2y=5 6x2y=16 Multiplying each term on both sides of the equation by 2 x2y=5 7x = 21 x = 3 solving for y 3x y = 8 98 = y 1 = y Pt(3,1) is the solution for this sytem



Solve The Following Systems Of Equations X Y 2 4 X 3 2y 5 Sarthaks Econnect Largest Online Education Community




Ex 3 4 1 Solve By Elimination And Substitution I X Y 5 2x 3y
Procedure for elimination method Multiply one or both of the equations by a suitable number(s) so that either the coefficients of first variable or the coefficients of second variable in both the become numerically equal Solve the following system of linear equations by elimination method x (y/2) = 4 and (x/3) 2 y = 5 Given XXXx −2y = 5 XXX2x − 3y = 10 Rewriting as augmented matrix XXX1 −2 5 2 −3 10XXX1 2 Subtracting 2 times the first row from the second row XXX1 −2 5 0 1 0XXX1 3 = 2 −2 × 1 Adding 2 times row 3 to the first row XXX1 0 5 0 1 0XXX4 3 = 1 2 × 3Xy=5;x2y=7 Try it now Enter your equations separated by a comma in the box, and press Calculate!




Hw 3 Due 9 27 Solve Each System Of Equations Chegg Com



How To Solve For X And Y In X Y 5 And Xy 6 Quora
The goal is to arrange that either the x terms or the y terms are opposites, so that when the equations are added, the terms eliminate The steps for the elimination method are outlined in the following example Example 1 Solve by elimination {2 x y = 7 3 x − 2 y = − 7 Solution The Questions and Answers of 04x 03y=17 07x02y=08 7(y 3)2(X 2)=14 4(y2) 3(x3)=2 X y/2=4 X/3 2y=5 solve this in two min From substitution, elimination,and cross multiplication method? Find an answer to your question Solve xy=5 And 2x3y=4 using elimination method prathikshasubba prathikshasubba Math Secondary School answered Solve xy=5 And 2x3y=4 using elimination method 2 See answers anveshasingh191 anveshasingh191 X y = 5 (




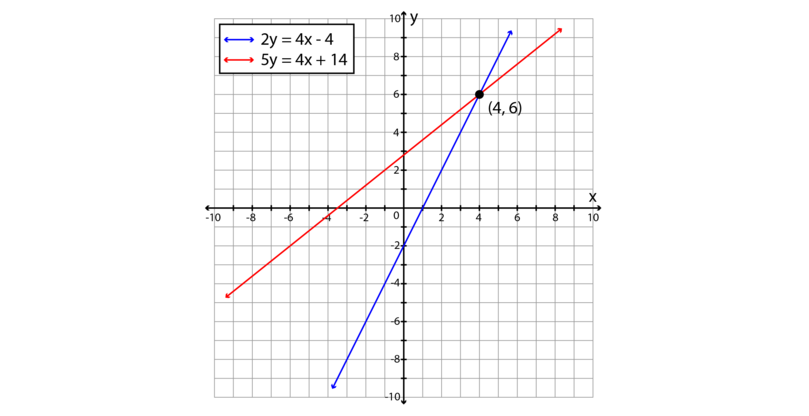
Solve 2x Y 5 And 3x 2y 8




Write The Augmented Matrix For Each System Do Not Chegg Com
We then find the generic solution By solving the second equation for y y and substituting it into the first equation we can solve for z z in terms of x x x 2 y − z = 1 y = 2 z x 2 ( 2 z) − z = 1 x 3 z = 1 z = 1 − x 3 x 2 y − z = 1 y = 2 z x 2 ( 2 z) − z = 1 x 3 z = 1 z = 1 − x 3Solving Linear Equations by Elimination Method Here we are going to see some example problems of solving linear equations in two variables using elimination method The various steps involved in the technique are given below Step 1 Multiply one or both of the equations by a suitable number (s) so that either the coefficients of firstUse the elimination method to solve the following system of equations x 3y – z = 2 x – 2y 3z = 7 x 2y – 5z = –21 algebra How to solve the system of equations below using elimination?




How Do You Solve X 1 2 Y 2 3 4 And X 2y 5 Socratic




Solving A System Of Equations Using A Matrix Precalculus Socratic
Steps for Solving Linear Equation x2y=5 x 2 y = 5 Subtract x from both sides Subtract x from both sides 2y=5x 2 y = 5 − x Divide both sides by 2 Divide both sides by 25 Answers Sathish thangaraj answered Solve using Gauss Elimination method X 2Y Z = 6 2X Y 3Z = 12 3x 2Y 4Z = 17 Thank Writer(a) 2x 3y = 12(i) and x y = 1(ii) (ii)×3 ==> 3x 3y = 3(iii) Now we can eliminate y by adding (i) & (iii) (i) (iii) ==> 5x = 15 so x=3



What Are X And Y From The System Equation 2x 3y 4 X Y 6 Quora




Elimination Method Day 1 Ppt Download
4x 6y = 7 asked in Linear Equations by Anika01 ( Solve by elimination method 03x 02y = 4, and 02x 05y = 75/17 Second question, also solve by elimination 005x 025y = 44, 015x 005y = 48 I thought I had a handle on solving by elimination, but somewhere along the line (especially where the fractions come in) I think in the second part of solving the equation I am messing upB = 2a1 10ab=5b2 math 2 Solve the following system using the elimination method 6x 2y = 5 12x 4y = math 116



Www Sedelco Org Site Handlers Filedownload Ashx Moduleinstanceid 4217 Dataid 2808 Filename Elimination method Pdf




If The Equation Kx 2y 5 3x Y 1 Has No Solution Then What Is The Value Of K Quora
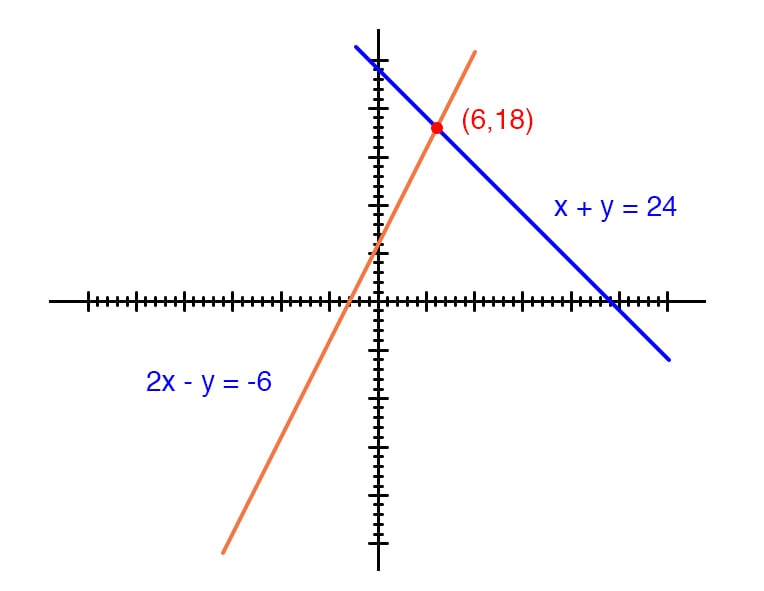
The simultanous equation calculator helps you find the value of unknown varriables of a system of linear, quadratic, or nonlinear equations for 2, 3,4 or 5 unknowns A system of 3 linear equations with 3 unknowns x,y,z is a classic example This solve linear equation solver 3 unknowns helps you solve such systems systematically\\begin{aligned}&x2y=10\\&2xy=5\end{aligned}\ > Ex 3 6 1 V And Vi 7x 2y Xy 5 8x 7y Xy 15 Please Help Me Answering The Following Problems 18 Chegg Com Exercise 43 1 Solve the following system of equations x 3 y = 14 − 8 x − 3 y = − 28 Answer ( 2, 4) To show that you have the option of which variable you choose to eliminate, let's try Example 43 1 a second time, this time eliminating y instead of x\(x y = 5 \\2x 3 y= 4 \) Steps Elimination method Best Answer 3x4y=11 5x2y=5 note that, if we multiply the second equation by 2 and add it to the first one, we can "eliminate" y So we have The Following System Of Eguat See How To Solve It At Qanda Solve The Simultaneous Equations 10 X Y 2 X Y 4 15 Solve this linear system using the elimination method 2x 3y = 4 3x – 2y = 6 Multiply the first equation by 2 and the second equation by 3, and then add them together to clear the equations of y 4x 6y = 8 9x – 6y = 18 Addition time (4x 9x) (6y – 6y) = (18 8) 13x = 26 x = 2 Plug x = 2 into one of the original equationsSubstitution 1 2 From eq 2, Substitute into eq 1,Question Solve the question by the method of elimination by substitution Question 3x4y= x2y=5 Answer by Fombitz() (Show Source) You can put this solution on YOUR website! Solve The Following Systems Of Equations X Y 2 4 X 3 2y 5 Sarthaks Econnect Largest Online Education Community X 2 2y 3 1 And X Y 3 3 Find X And Y Values Using Elimination And Substitution Method Youtube X \displaystyle x x in the first equation, 1 We can add the two equations to eliminate x \displaystyle x x without needing to multiply by a constant x2y=−1 −xy=3 3y=2 x 2 y = − 1 − x y = 3 3 y = 2 Now that we have eliminated x \displaystyle x x,Free PreAlgebra, Algebra, Trigonometry, Calculus, Geometry, Statistics and Chemistry calculators stepbystep Example Solve for x and y if 3x 2y = 4 and x 4y = 3 Answer x = 1 and y = 1/2 Step 1 Label the equations Label the equations A and B (A) 3x 2y = 4 (B) x 4y = 3 Step 2 Isolate one of the variables To use the substitution method, we need to isolate one of the variables We will isolate variable x in equation B in this example x Solving Simultaneous Equations The Substitution Method And The Addition Method Algebra Reference Electronics Textbook Ch 3 5 Elimination Multiplication Ppt Download 1) Solve by the elimination method 4x12y=4 4x12y=5 2) Write interval notation for the set {x 1 > x > 6} 3) A cellular phone company offers a contract for which the cost C, in dollars, of t minutes of telephoning is given by C = 025(t600) 6295, where it is assumed that tThis is basic linear algebra Solve a system of two linear equations in two unknowns (variables) Use the (GaussJordan) elimination method to eliminate one variable linear system 1 math x 2y = 5/math 2 math3x y = 1/math EliminateThe method of elimination is a useful tool that will be used here in order to get the solution or a pair of values of x x and y y such that both the equations satisfy simultaneously In this Solve The Following Systems Of Equations 3 X Y 2 X Y 2 9 X Y 4 X Y 1 Sarthaks Econnect Largest Online Education Community Ex 3 3 1 Solve By Substitution Method I X Y 14 Ex 3 3 Solve by Addition/Elimination xy=3 , xy=7, Multiply each equation by the value that makes the coefficients of opposite Simplify Tap for more steps Simplify Tap for more steps Apply the distributive property Rewrite as MultiplyOr click the example About Elimination Use elimination when you are solving a system of equations and you can quickly eliminate one variable by adding or4x 3y = 8 x 2y = 13 Solve the system of equations using the elimination method In these equations, neither the "x" or the "y" will cancel out, we will have to do an extra step first THINK of what you can multiply one of the equations by so that one of the variables could cancel out Solve The Following System Of Equations By Using The Method Of Using Matrix Method Solve The System Of Equations 3x 2y 2z 3 X 2y 3z 6 2x Y Z 2 Studyrankersonline High School Math Solutions – Systems of Equations Calculator, Elimination A system of equations is a collection of two or more equations with the same set of variables In this blog post, So we have 3y = 18 Divide both sides by 3 and we find that y = 6 Using either one of the equations I'll pick the second one substitute 6 for y to find x Thus, x 6 = 5 Subtract 6 from both sides, and we get that x = 1 Therefore, x = 1Solve by Addition/Elimination 3x2y=16 2x2y=4 3x 2y = 16 3 x 2 y = 16 2x − 2y = 4 2 x 2 y = 4 Add the two equations together to eliminate y y from the system If X Y 3 X Y 1 Then What Is X Y Quora Find The Values Of X Y Z In The Following System Of Chegg Com Solve the system of equation by using elimination by multiplication x4/5y=9 4/5 and 14x4y=46 asked in ALGEBRA 1 by andrew ScholarSolve the following systems of equations x y/2 =4 x/3 2y =5 Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get`x = 1 2 xx 15/5 = 1 30/5 = 90/5 = 18` ∴ Solution is x = 18 and y = 15 Concept Methods of Solving Simultaneous Linear Equations by Elimination Method Solving Simultaneous Equations Equations And Inequalities Siyavula If X Y 3 X Y 1 Then What Is X Y Quora Elimination method First multiply one or both the equations by some suitable nonzero constants to make the coefficients of one variable numerically equal then add or subtract one equation from the other so that one variable gets eliminated (i) What is the Known?Avail 25% off on study pack Solved X 7 Y 3 5 X 2 Y 9 6 By Elimination Method Brainly In 7 Y 3 2 X 2 14 4 Y 2 4 X 3 44 Solve Equation Using Elimination Method Brainly In How Do You Solve 2x 3y Z 1 3x Y 2z 12 And X 2y 3z 5 Socratic Canvas Bham Ac Uk Courses Files Download Verifier Olsyulszmw31bkuumjmm1h3moiw4myavdszsni9s Wrap 1 2x 5y 4 And 3x 2y 16 0 Find X And Y Brainly In J19 Solving A System Of Equations Using A Matrix Precalculus Socratic A E A X Y Z 11 X Y 2 3 Homeworklib Solve The Following System Of Equations 1 2 X 2y 5 3 3x 2 3 Systems Of Linear Equations 7 Solve The Following System Of Linear Equations Chegg Com Solving Linear Systems For Solving Each Pair Of Equations In This Exercise Use The Method Of Elimination By Equating Coefficients Begin Array L 7 Sqrt 3 2 Y 9 X Text 2 3 X Y 23 Frac X 3 Frac Y 4 4 End Array Link Springer Com Content Pdf m 3a978 1 349 3 2f1 Pdf Solve The Following Systems Of Equations 1 2 X 2y 5 3 3x 2y 3 2 5 4 X 2y 3 5 3x 2y 61 60 Sarthaks Econnect Largest Online Education Community Elimination Method Day 1 Ppt Download Solve The System Of Linear Equations Using The Elimination Method X 4y Z 18 3x Y Homeworklib Solve The Following Systems Of Equations 1 2 X 2y 5 3 3x 2y 3 2 5 4 X 2y 3 5 3x 2y 61 60 Sarthaks Econnect Largest Online Education Community The Substitution Method Ex 3 4 1 Solve By Elimination And Substitution I X Y 5 2x 3y How Do You Solve X 2y 6 And X Y 2 Socratic 10 X Y 2 X Y 4 And 15 X Y 5 X Y 2 P S 1 4 Q2 Linear Equation In Two Variables Youtube Ex 3 6 1 V And Vi 7x 2y Xy 5 8x 7y Xy 15 Elimination Method Simultaneous Linear Equations Siyavula X Y 2 4 X 3 2y 5 Plz Solve This By Elimination Method Brainly In Mfm2p Ex 3 4qno1 1 Solve X Y 5 2x 3y 4 By The Elimination Method Youtube Solved 8 Solve The Linear System Of Equations 2 X Y 1 U Chegg Com 0 4x 0 3y 1 7 0 7x 0 2y 0 8 7 Y 3 2 X 2 14 4 Y 2 3 X 3 2 X Y 2 4 X 3 2y 5 Solve This In Two Min From Substitution Elimination And Cross Multiplication Method Edurev Class 10 Question Solve The Following N Frac X 3 Frac Y 6 Frac 4 X 3 2 Y N X 4 Y Frac X Y 10 Ml Aggarwal Solutions For Class 9 Maths Chapter 5 Simultaneous Linear Equations How To Solve Using The Gauss Elimination Method Y Z 2 2x 3z 5 X Y Z 3 Quora Systems Of Linear Equations X Y 2 4 X 3 2y 5 Solve It By Elimination Method Brainly In Http Www Math Utep Edu Faculty Cmmundy Math 2301 Solution Manual Pdf Solve For X And Y X 1 2 Y 1 3 9 And X 1 3 Y 1 2 8 Brainly In Solved By Elimination Method 2x Y 5 And 3x 2y 8 Brainly In Solve X Y 7 And 3x 2y 11 Ex 3 4 1 Solve By Elimination And Substitution I X Y 5 2x 3y 2 X Y 3 X Y 1 8 X Y 7 X Y 5 6 Solve X And Y Youtube By The Substitution Method Solve The Linear Equation That Is 8 X 5 Y Is Equal To 9 And 3 X 2 Y Is Equal To 4 Mathematics Topperlearning Com Usvpr6ll R D Sharma Solutions Class 10th Ch 3 Pair Of Linear Equations In Two Variables Exercise 3 3 Class 10 Linear Equations In Two Variables 1 2 X 2y 5 3 3x 2y 3 2 And 5 4 X 2y Youtube Solve The Following Pair Of Linear Equations By The Elimination M Cramer S Rule To Solve A System Of 3 Linear Equations Example 2 Youtube 10 X Y 2 X Y 4 15 X Y 9 X Y 2 By Substitution Method Brainly In Answers Solve By Elimination Method X Y 2 4 X 3 2y 5 Brainly In Solve 3x 2y 11 And 2x 3y 4 Solve For X And Y 2 3x 2y 3 3x 2y 17 5 5 3x 2y 1 3x 2y 2 5 1 Exercises 9 What Is The Center Of The Ellipse Math Frac X Y 2 2 9 Frac X Y 2 16 1 Math Quora Solve The System Of Equations 3x 3y 2z 1 X 2y 4 10y 3z 2 And 2x 3y Z 5 Answer Mathematics 1 Question Answer Collection Revision 1 Simultaneous Linear Equations In Two Unknowns A Pair Solve X Y 3 And X 3 Y 2 6 By Substituting Methos Scholr Maths Guru Please Help Me Solve This Simultaneous Equations For My Young Photo Education 2 Nigeria Find The Circumcenter Whose Sides Are 3x Y 5 0 X 2y 4 0 5x 3y 1 0 Quora Solve The Following Pair Of Linear Equation By Substitution Method 3x 2y 7 0 4x Y 6 0 22 4 3x 6 317 3 2x 3y 11 4 X 2y 8 6 26 Chegg Com The Solution Of 2x Y Z 1 X 2y 3z 1 3x 2y 4z 5 Is 1 1 2 3 2 1 2 3 3 1 3 2 4 Youtube Solve The Following Systems Of Equations 2 X 3 Y 2 4 X 9 Y 1 Sarthaks Econnect Largest Online Education Community Link Springer Com Content Pdf m 3a978 1 349 3 2f1 Pdf 7 Solve The Following System Of Linear Equations Chegg Com Systems Of Equations With Substitution 2y X 7 X Y 4 Video Khan Academy Ssc Mathematics Chapter 4 Pair Of Linear Equations In Two Variables Solving A System Of Equations Using A Matrix Precalculus Socratic 3x 2 5y 3 2 And X 3 Y 2 13 6 Solve Using Substitution Method Youtube X 7 Y 3 5 X 2 Y 9 6 By Elimination Method Novocom Top The Elimination Method Graph Graph Inequalities With Step By Step Math Problem Solver 4 3 Systems Of Linear Equations In Three Variables Solve 3x 4y 10 2x 2y 2 By The Method Of Elimination


































































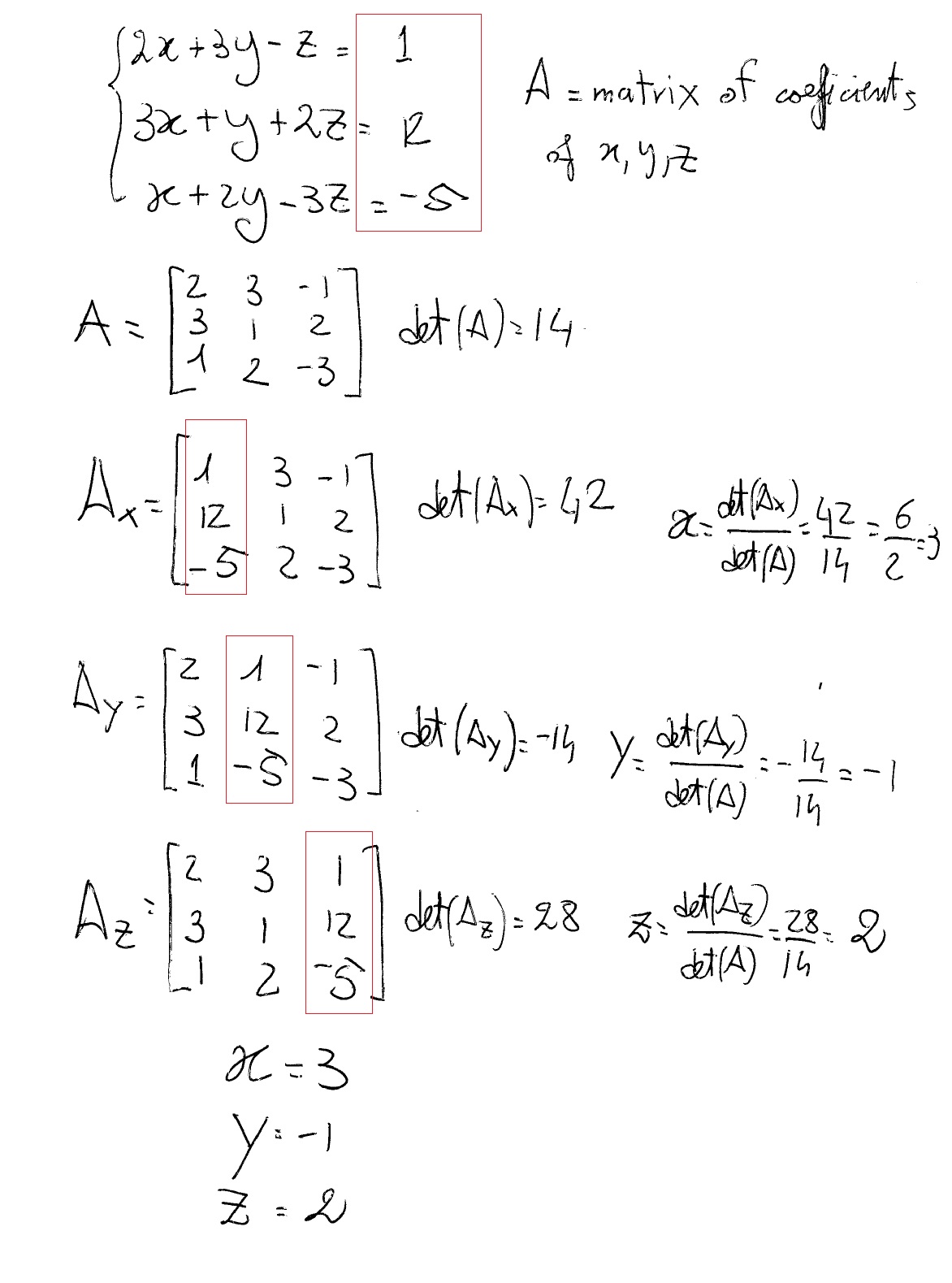






















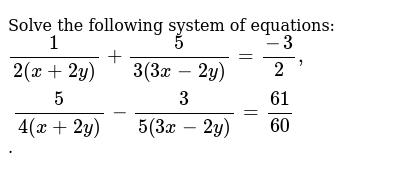











































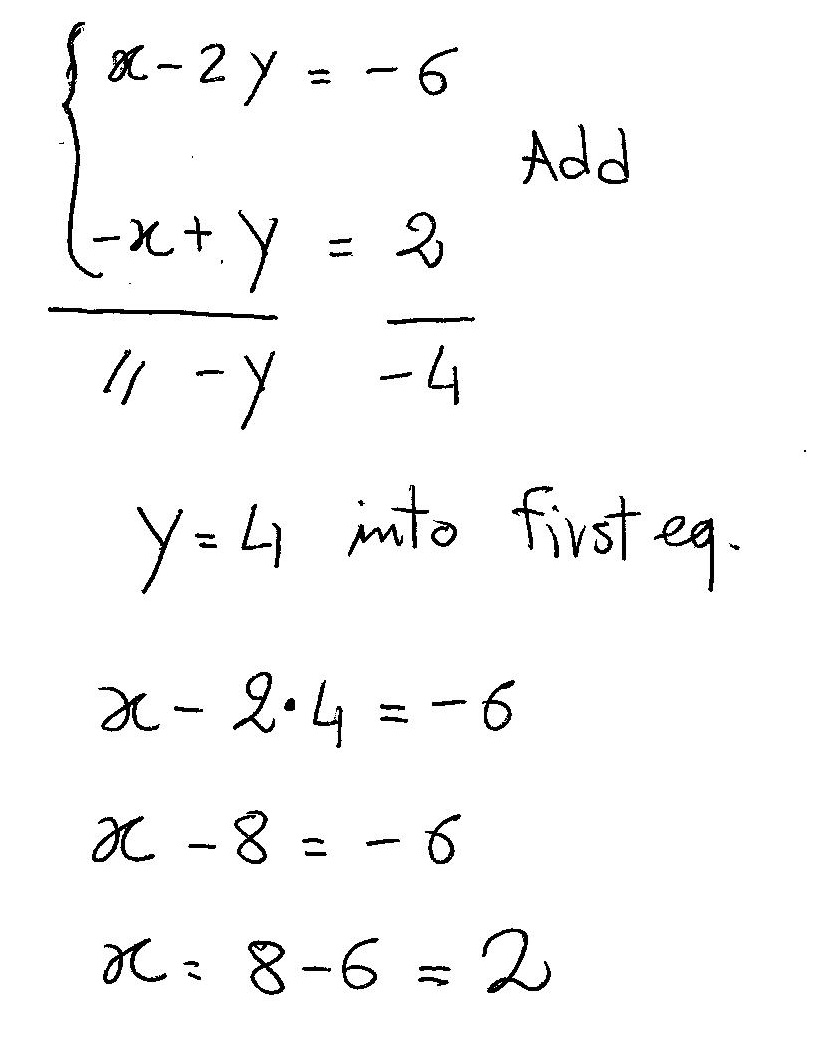



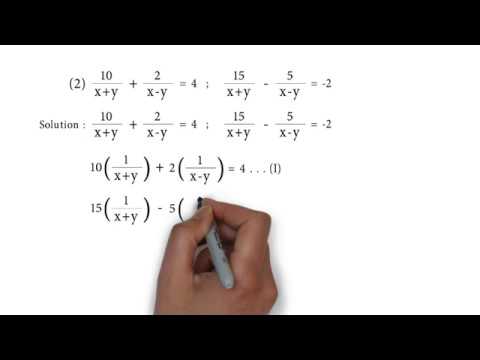






































































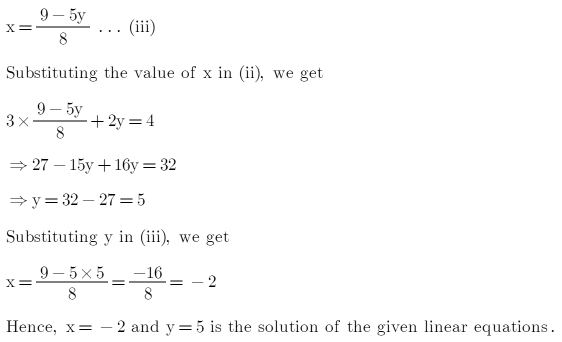




























































































































0 件のコメント:
コメントを投稿